通过钻孔应变计测量残余应力的标准试验方法¹

本标准以确定的标识E837发布，标识后的数字表示原稿录用年份，或如果有过修订的情况，最近一次修订的年份。圆括号中的数字表示最近一次审核的年份。上标epsilon艾普西龙 (e)表示最后一次修订或审核前的编辑性修改。

ε¹——方程式17和18，章节9.2.2，9.2.3,11.2.5,11.2.6和表2于2002年1月以编者身份upated。

引  言

钻孔应变计法用于测量某种材料近表面的残余应力。这种方法包括在表面上粘贴应变计、在应变计附近钻孔，并测量减小的应力。所测应变通过一系列的方程式与减小的主应力相关。

1、范围

1.1  这种试验方法包括测定等方性的（各向同性）线弹性材料的近表面残余应力的程序。尽管这种概念是很笼统的，但是这里所描述的试验方法在那些应力对深度并不十分敏感并且不会超过屈服强度的一半的情况下是适合的。这种试验方法经常被描述为“局部破坏性的”，是因为它所导致的破坏是非常局部的，而且在很多情况下并不会明显影响试样的使用。相比之下，其他许多测量残余应力的力学方法则会严重破坏试样。但是由于这里描述的试验方法依然会导致一些破坏，因此它只能被用于那些情况下：在试样有加工余量的地方或者引入较浅

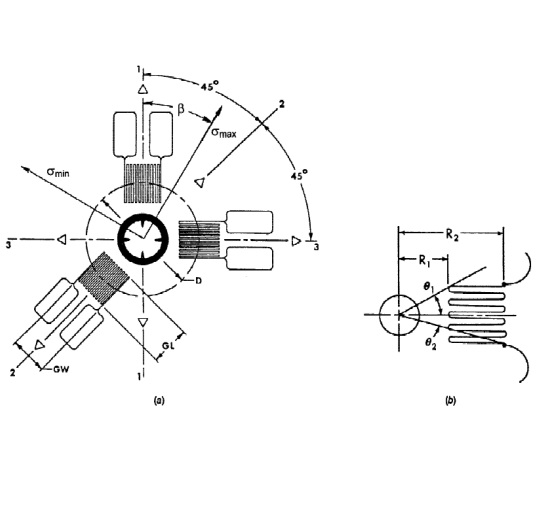
图1 显示典型的钻孔法专用三元素顺时针应变花几何形状的示意简图

¹ ASTM E28力学试验委员会拥有本试验方法的最终解释权，并由E28.20残余应力测量小组委员会负直接责任。

现行版本于2001年10月10日通过，2001年11月颁布。起初以E 837-81颁布。此前最新版本为E 837-99。

小洞也不会明显影响试样的使用的地方。

1.2  这个标准并不声称指出了所有对安全性的担心，若有的话，也是联系到它的使用。在建立适当的安全和健康操作并在使用之前确定调整限制条件之后的应用范围，是这个标准的使用者的责任。

2、引用文件

2.1 ASTM标准

E 251  金属结合电阻应变计工作特性的试验方法²

3、试验方法摘要

  3.1  图1示意说明的是一个有三元或多元的普通类型的玫瑰形应变花被放置在考虑中的这个区域。应变计的这个编码方案按照顺时针（CW）习惯（1）³。

  备注1——图1所示的应变花所用的应变计编号习惯不同于一些普通用途应变花和其他一些类型电阻应变花所用的逆时针习惯（CCW）。如果使用的是一个具有CCW的应变花，那么本试验方法中所描述的残余应力的计算方法依然适用。唯一的变化是在最拉伸的主应力方向上的反转。关于这一变化的描述见备注7。其他所有方向残余应力的计算不受影响。

  3.2  在应变花几何中心钻一个深度为0.4D（应变计圆周平均直径）的小孔。

  3.2.1 包围在钻孔周围的残余应力得到释放。释放的应变被一个合适的应变记录仪器测量。在紧邻小孔的地方，当小孔深度接近0.4D的时候应变几乎完全释放。

  3.3  图2显示了残余应力和一个当材料上钻入一个小孔时典型的表面应变释放的示意图。表面应变释放与释放的主应力按照下边的关系相关：

ε_r  =  (A^ˉ + B^ˉ cos2β) σ_max

+ (A^ˉ - B^ˉ cos2β) σ_min         (1)

这里：

图2 符号释义

ε_r   = 使用中心位于P点的放射状取向的应变计测量所得到的释放应变。

A^ˉ,B^ˉ = 向量

σ_max  = 最大拉应力

σ_min  = 最小（最大压缩的）主压应力

β    = 顺时针测量1号应变计与σ_max的

夹角

D    = 应变计中心所围圆周直径

D₀   = 钻孔直径

3.3.1 下边的方程式可以用来评估一个给定弹性性能的材料的恒量A^ˉ和B^ˉ。

A^ˉ= – a^ˉ (1+v) / (2E)         (2)

B^ˉ= – b^ˉ / (2E)              (3)

这里：

E  = 杨氏模量，

v  = 泊松比，

a^ˉ和 b^ˉ 是无量纲的，几乎是材料的独立恒量（见备注2）。对于薄试样上的通孔和厚试样上的盲孔而言，两者所适用的这两个恒量值略微不同。

备注2——无量纲系数a^ˉ和 b^ˉ随孔深变化而变化，如表1所示。它们几乎是材料独立的，并不依赖于杨氏模量E，而且当泊松比在0.28~0.33范围内的时候它们的变化不到1%。对于薄板上的通孔a^ˉ与泊松比是相互独立的。

3.3.2 释放应变ε₁，ε₂和ε₃分别由如图1所示相对应编号的应变计测得。对于专业应

² ASTM标准年度汇编，Vol 03.01。

³ 圆括号中的粗体数字在本试验方法结尾的参考资料列表中被提及。

用，3对应变计通常沿方向1-2-3布置（见5.2.3）。测量这3个参与应变为计算主应力σ_max和σ_min以及它们的方向β。

3.3.3 在图2中因为图示清晰的缘故，在小孔四周整个区域内的主残余应力σ_max和σ_min被暂时表示为均衡的。事实上，使残余应力在如此大的范围内均衡化是没有必要的。释放的表面应变仅仅依赖于小孔边缘的初始主应力（2）。小孔边缘的应力不会影响释放应变。正因如此，钻孔法是一种非常局限性的残余应力测量方法。

3.3.4 假设小孔边缘以内的初始应力的变化是很小的，并且随深度的变化也是可忽略的。小孔以外位置上的初始应力的均匀化是没有必要的。

4、意义与应用

4.1  残余应力存在于几乎所有的构件中。它们可能以生产工序的结果存在，或者在构件的使用过程中产生。许多情况下残余应力是构件失效的主要因素，尤其是那些

表1 系数a^ˉ和b^ˉ的数值

在经受交变载荷或者腐蚀性环境的情况。残余应力也有可能是有益的，比如，喷丸处理得到压应力。见表1。

5、应变计

5.1  一套应变花包括三个单独的或者成对的应变计栅格应该被用到。

备注3——建议应变计是与试验方法E 251相一致的标准化的。

5.1.1 应变计应该排列成一个圆圈，与应变花的中心等距。

5.1.2 主应变计的轴向应该朝向以下三个方向的任意一个：（1）一个参考方向；（2）与参考方向呈45°或135°夹角；和（3）垂直于参考方向。方向（2）把方向（1）和（3）二等分，（见图1）。

5.2  可以使用几种不同的标准应变花来扩大残余应力测量的应用范围。⁴图3展示了三种不同的应变花类型。

5.2.1 图3（a）所展示的A型应变花，被Rendleer和Vigness第一次介绍（3）。这种型号可用到好几种不同的尺寸，建议作为普通用途使用。

5.2.2 图3（b）所展示的B型应变花，所有应变花栅格都位于同一个方向上。当需要在一个障碍旁边进行测量时这种设计是非常有效的。

5.2.3 图3（c）所展示的C型应变花，这款具有特殊用途型号的应变花具有3对相反的应变计栅格连接成3个半桥。这种型号主要用于那些需要大应变敏感度和高热稳定性的场所（19）。

备注4——Rendler和Vigness（3）首次提议将钻孔应变花型号标准化。标准化应变花设计的应用大大简化了残余应力的计算。

5.3  应变计圆圈的中心在钻孔前后都应该清晰可辨。

5.4  应变计的应用（粘贴，布线，防护涂层）需要严格遵守制造商的建议，并要确保在钻孔操作中对应变计栅格的保护。

5.5  应变计残留物应该是永久连接的，并要核实安装的稳定性。比较合适的对地电

图3  钻孔应变花

阻是至少20000MΩ。

6、测量仪器

6.1  记录应变的测量仪器应该拥有±2×10^?6的分辨率,测量的稳定性和再现性应至少为±2×10^?6。每只应变计的铅丝线应尽量短以便于适用，三线温度补偿线路（4）应该使用A型和B型应变花。半桥线路需要使用C型应变花，相对应输出的结果分别用ε₁，ε₂和ε₃标明。

备注5——通常，应该对那些被证明引起不明显残余表面应力的方法的表面准备工作进行限制。

7、试样准备

7.1  粘贴应变计之前，应该按照粘贴应变计的粘结剂制造商的建议来进行表面准备工作。

7.1.1 必须进行彻底的清洁和去污处理。

7.1.2 使用应变计需要光滑的表面。

8、步骤

  8.1  钻孔：

⁴ 这些图样中的应变计型号由Measurements Group, Wendell, NC.公司制造。

8.1.1 为保护应变计栅格，在小孔外缘与应变计栅格的最后一圈之间应至少留有0.012in(0.30mm)的余地。对这个余地的要求限制了小孔的直径D₀的最大允许值。最小推荐孔径为最大允许值经的60%。表2列出了几种常见应变花类型的推荐孔径范围。

备注6——随着D₀/D比值的增加，这种方法的敏感度近似等于(D₀/D)²。通常因为敏感度增加而建议使用直径较大的孔。

8.1.2 无论钻孔直径有多大，小孔的中心与应变计圆圈的同心度应该在±0.004D或±0.001in(±0.025mm)的范围内。因钻孔未对准造成的错误会使应力计算产生明显的误差。为避免这些误差，建议使用光学装置对工具支撑物进行对中。图4展示了一种适合的装置⁵。

8.1.3 选择合适的钻孔操作和工具以减小或消除小孔周围区域引入的的塑性变形。

8.1.3.1 有研究和报道指出的几种钻孔工艺适合作为钻孔方法：

((1) 磨料喷射加工⁶，这是一种使用包含有细小磨料微粒的高速气流通过一个小直径喷嘴对准工件进行钻孔的方法，被成功使用(5,6)。不过这种方法不适用于类似于铜的较软材料(7)。

((2) 使用空气涡轮进行高速钻孔也在这项应用中被成功使用(8)。这个工艺被认为是普遍适用的，除了钨铬钴硬质合金等极硬材料之外(7)。

((3) 平铣刀，硬质合金钻头，以及改进型平铣刀在许多研究中被成功应用(3,9，10,11)。不过比较起来使用磨料喷射加工或者高速钻孔平铣刀进行低速钻孔更合适。

由于被各种钻孔方法所创造出的残余应力都会对结果的精确度产生不利影响，因此当没有可供参考的前期经验时，建议对所选方法进行验证。这个验证应包括在一个具有相同的名义成分的无应力试样上使用与检测过程中所用相同的应变花，然后钻一个孔。如果钻孔方法满足要求，那么钻孔所产

(a)对中——工具引导与应变计圆圈对中。    (b)小孔研磨——在移动对中显微镜之后，插入钻孔工具。

图4  一种工具支撑物对中设备

⁵一种由Measurements Group，Wendell，NC生产的用于对中的设备。

⁶摩擦喷射加工工具可以从S.S. White，Piscata- way，NJ获得。

表2  应变花尺寸和推荐的小孔尺寸

生的应力将会很小。

备注7——最普遍的应用接近于获取无应力试样是退火热处理方法(5，6，7，15，16)。近来的研究(18)表明电火花加工也是值得考虑的一种从大块儿材料上切取小的无应力试样的方法。一般来说，试样越小其所要承受的残余宏观应力就越小，当然，它的尺寸必须能够与应变计花相适应。

备注8——如果钻孔方法所导致的可量度水平上的残余应力是可再生的，需要考虑实验性的校准（见9.3）。

8.1.3.2 当使用最终研磨时，使用非常轻并缓慢的轴向进给继续进行，以允许热量有足够的时间散失。

8.1.4 在恒温下开展钻孔试验。

8.2  在开始钻孔操作前从每一个应变计上读取零值。然后，开始钻孔使用接下来的两个步骤之一，这取决于试样的厚度。

8.2.1 试样的厚度大于1.2D被认为是“厚”。对于这种试样，获得8组应力读数ε₁、ε₂、ε₃，从孔深每增加0.05D到最终孔深0.4D。其他类似的增额也可接受；不过，它们由于需要额外插入或推算表1中的校准恒量而不便于计算。

8.2.2 试样的厚度小于0.4D被认为是“薄”。对于这种试样，当小孔钻穿整个试样厚度的时候，获取一组应力读数ε₁、ε₂、ε₃。

8.2.3 中间的情况当试样厚度在0.4D到1.2D之间的时候不在标准试验方法的范围。对于这种试样可以得到一个近似的结果，通过使用通孔并修改表1中给出的“盲孔”和“通孔”校准数据。用这种方法得到的残余应力结果应该注明“非标准值”或“近似值”。

8.3  对每一组测得的应力值ε₁、ε₂、ε₃计算下边的合成应力：

p = (ε₃ +ε₁) /2                    (4)

q= (ε₃ -ε₁) /2                     (5)

t = (ε₃ +ε₁- 2ε₂)/2                 (6)

8.3.1 当用“厚试样”工作时，应该做一个试验以核实残余应力在孔的深度内是均匀的。此时，找出数值较大的一组合成应变q或t。当孔深等于0.4D的时候，把每一组合成应变p以及q和t较大的一个表达成它们数值的百分数。将这些应变的百分数与对应的(孔深/D)绘成曲线。这个图表应该产生类似于图5所展示的曲线的数据点(12)。数据点偏离图5中的曲线超过±3%表示每一个实质应力在材料厚度方向是不均匀的，或者应变测量出现错误。不论发生哪种情况，在使用这里所描述的步骤时，测得的数据都不能用于残余应力计算。其他出版物比如Ref (21)，给出了用于评估来自钻孔应变数据增量产生的不均匀的残余应力的方法的细节。然而，这样的计算不属于本试验方法的范围。

备注9——这种图示的试验不是应力场均匀性的灵敏指标。具有明显不均匀应力场的试样会产生大体上类似于图5所示的那些百分比释放应变曲线。这个试验的主要目的是为了鉴定非常不均匀的应力场和应变测量错误。这个应力均匀性试验只有在使用“厚”试样时有用。

9、应力计算

9.1  薄试样

9.1.1 在试样较“薄”的时候，只需要单独的一组ε₁、ε₂和ε₃测量值来计算主残余应力的大小和方向。这些应力被假定在试样的整个厚度方向上是均匀分布的。

9.1.2 最大拉伸或最小压缩主应力σ_max位于图1中应变计1方向顺时针测得的β角的位置。同样，最小拉伸或最大压缩主应力σ_min位于图3中应变计3方向顺时针测得的β角的位置。

9.1.3 使用下式计算β角：

β=1/2 arctan（t/q）              (7)

9.1.4 使用普通的一元arctan函数直接计算β角，比如对于一个简单的计算就发现，会得到一个±90°的误差。正确的角度可以通过使用二元arctan函数得到（有些计算机语言中的ATAN2函数），此时分子和分母都参与计算。作为选择，如果必要可以通过将一元函数计算得到的结果±90°来调整来使β位于下表所确定的合适的范围：

9.1.5 一个正的β值，假定β=30°，表示σ_max位于应变计1方向顺时针30°的位置。一个反的β值，假定β=-30°，表示σ_max位于应变计1方向逆时针30°的位置。

9.1.6 通常，σ_max的方向会与数值上完全相反（压缩）的释放应力的方向接近一致。当q和t同时等于0的时候β角没有意义。

备注10——在9.1.2中定义的顺时针测量β角的方向仅应用于具有CW编号方式的应变花，比如在图1中的插图。相反的测量方向应用于CCW应变花。在这个应变花里，应变计1和3的几何位置依据CW情况互相调换位置。新的应变计1成为参考应变计。对于一个CCW应变花，一个正的β值，假如β=30°，表示σ_max位于应变计1逆时针30°的方向。一个负的β值，假如β=-30°，表示σ_max位于应变计1顺时针30°的方向。所有其他方向的残余应力计算对CW和CCW应变花完全相同。

9.1.7 使用下式计算应力σ_max和σ_min：

σ_min, σ_max=-[p/a^ˉ(1+v)±√(q²+t²)/b^ˉ]E  (8)

  这个方程式中的负平方根与σ_max相关联是因为方程8右侧的负号。一个拉伸的(+)残余应力会产生一个压缩的(-)释放应变。

9.1.8 使用表1确定与孔径和所用应变花类型相对应的校准常数a和的数值。

9.2  “厚”试样

9.2.1 在“厚”试样的情况下，每一组ε₁，ε₂，ε₃测量值都被用于计算主残余应力的大小和方向。假设贯穿整个孔深的这些应力是均匀的。

备注11——与9.1所描述的只用一组在0.4D时的ε₁，ε₂，ε₃测量值来进行计算也是可以的。这样的计算对于快速给出一个残余应力估计值是很有用的；但是，9.2中描述的求平均值方法应该是首选，因为这种方法使用了所有的应变数据，并且显著地降低了随机应变测量误差的影响。

9.2.2 对于每一个孔深所对应的8组ε₁，ε₂，ε₃测量值，使用表1确定与孔径和所用应变花类型相对应的校准常数a和b的数值。表中的这些数值来源于有限元分析(14)，被发现与实验结果非常一致。

9.2.3 使用下边的公式计算与三个合成应

图5 典型的厚度方向上应力均匀分布试样的应变百分值与对应的深度二维图，（a）A型应变花，（b）B型应变花，（c）C型应变花

变p，q和t相对应的合成应力P，Q和T(20)：

P = – E × (∑a^ˉ· p) / (∑a^ˉ2) / (1+ v)    (9)

Q = – E × (∑b^ˉ· q) / (∑b^ˉ2)         (10)

T = – E × (∑b^ˉ· t) / (∑b^ˉ2)          (11)

9.2.4 使用下式计算β角：

β=1/2 arctan (-T/-Q)             (12)

          =1/2 arctan (∑b^ˉ·t /∑b^ˉ·q)

通过使用类似的方式评估“arctan”函数，β角可以在正确的象限内被替换为9.1.3中所描述的那些。

9.2.5 利用下式计算应力σ_max和σ_min：

σ_max, σ_min＝P±√(Q²+T²)          (13)

9.3  实验校准

9.3.1 如有必要，把应力σ_max和σ_min和测得的应变ε_i联系起来的常数a和b可以通过使用一个校准实验来确定。

当对“薄”试样（厚度不到0.4D）进行校准时，使用与真实试样相同厚度的试样。当对“厚试样”进行校准时，厚度要求为T，1.2D或者更大。

9.3.2 在钻孔之前，应用校准力经过五个相等的递增值达到最大力。这个最大力产生的应力σ_cal不能超过测试材料三分之一的屈服应力。

9.3.3 使用方程4-6计算与应变ε₁，ε₂和ε₃相应的合成应变p，q和t。P，q，t的曲线对应于外加应力。这些曲线应该是直线。确定它们的斜率gp，gq，和gt。

9.3.4 当使用“薄”试样工作时，钻一个通孔并按照五个相同的载荷增量达到最大力的序列重复应变的测量。

9.3.5 当使用“厚”试样工作时，以0.05D的增量直到最大值0.4D的一系列8个深度钻一个盲孔。在每一次孔深增加后，按照五个相同的载荷增量达到最大力的序列重复应变的测量。

9.3.6 从每一个孔深的p，q和t的斜率里减去在对应的每一个孔钻取之前测得的斜率：

(gp)_cal  =  (gp)_hole – (gp)_before       (14)

(gq)cal  =  (gq)_hole – (gq)_before      (15)

(gt)_cal  =  (gt)_hole – (gt)_before        (16)

在方程(9)-(12)中使用到的8个深度的常数a和b的校准值为：

a^ˉ = -2(gp)_cal × E / (1+v)          (17)

b^ˉ = -2√((gq)²_cal + (gt)²_cal) × E      (18)

10、报告

10.1  报告须包括以下内容：

10.1.1 试样描述/说明，

10.1.1.1 材料，

10.1.1.2 相关力学性能，

10.1.2 应变计位置，

10.1.3 所用应变计的规格型号，

10.1.3.1 应变计几何尺寸，

10.1.4 钻孔方法，

10.1.5 每个应变计的应变对应深度图表，

10.1.6 作表列出所有位置的应变值ε₁，ε₂和ε₃，以及，

10.1.7 作应力表格列出所有位置应变的方向。

11、精度和误差

11.1  误差：

  由这种方法所决定的残余应力可以预料到存在一个不超过±10%的误差，假如1.1所设定的条件得以应用以及钻孔技术不会在材料中诱发显著的机械加工应力(6,15)。最难以实现的条件应该是要求残余应力不能随深度明显的变化。残余应力通常被那些将能量卷入并贯穿物体表层的各种各样的制作、成型加工、焊接或其他生产工艺所诱发。因此，在表层附近通常存在有应力梯度，而且在深度范围内均匀不变的残余应力被认为是极少遇到的。如果一个明显不均匀的应力分布未被发现，那么误差可能远超过10%，并且朝向低估最大应力值的方向。

11.2  精确度:

11.2.1 一个循环试验程序(16)在经过预先应力释放处理的AISI 1018碳钢试样上被执行。高速，低速，和空气研磨钻孔方法被使用。合计，由八个实验室在8个名义上完全相同的试样上得到的测量值，根据所有26个测量值的平均值给出了一个2.0ksi (14MPa)的标准偏差。

11.2.2 一个循环试验程序(17)在经过预先应力释放处理的304不锈钢试样上被执行。总计，46个名义上完全相同的试样由35个实验室使用各种方法进行试验。46组使用高速钻孔和空气研磨钻孔方法产生的残余应力测量值，对于任何一种钻孔方法的平均值产生了标准差不超过1.7ksi(12MPa)的偏差。6组使用低速钻孔方法得到的测量结果不包括在内。

11.2.3 在有压力试样中得到的结果的多样性，相对应的与在无应力试样上观察到的情况相比，可以预料到是非常大的。一个正在由实验力学学会残余应力技术部计划开展的，在有应力不锈钢试样上进行的循环试验程序，ASTM E28.20小组委员会也参与其中。

11.2.4 应用于碳钢和不锈钢的对试验方法准确度的评估不适用于那些显现出机械性能特征非常不同于钢的甚至彼此不同的材料。高速钻孔技术被报道适合于不同种类的材料，比如铜合金，铝合金，锆合金和硬质合金(7)。

11.2.5 方程9-11降低了随机实验误差对结果的影响，并提高了精确度。随机实验误差独立于钻孔深度因为事件而出现，比如应变读数误差，应变计异常，以及实验环境改变等。在方程9-11中使用的最合适的应变数据平均技术可以调节多数的随机实验误差，但除了明显的应变错误(20)。

11.2.6 对于给定的应力水平，与使用三元A型和B型应变花相比，使用C型六元应变花可以增加电信号输出。电信号灵敏度的增加可以提高钻孔过程中测量值的准确度。不过，使用六元应变花会导致安装误差和费用增大。对于常规工作，A型和B型应变花就可以代表性地给出令人满意的结果。C型应变花适用于较精确的应用和针对低导电性材料进行操作的场合。

12、关键词

12.1  钻孔法；残余应力测量；应变计；应力分析

参 考 文 献

(1) Perry, C. G. “Data-Reduction Algorithms for Strain-Gage Rosette Measurements,” Experimental Techniques, Vol 12, No. 5, 1989, pp. 13-18.

(2) Schajer, G. S.,“ Application of Finite Element Calculations to Residual Stress Measurements,” Journal of Engineering Materials and Technology, Transactions, ASME, Vol 103, April 1981, pp. 157-163.

(3) Rendler, N. J., and Vigness, I., “Hole- Drilling Strain Gage Method of Measuring Residual Stresses,” Experimental Mechanics, Vol 6, No. 12, 1966, pp. 577-586.

(4) Perry, C. C., and Lissner, H. R., Strain Gage Primer, McGraw-Hill Book Co., Inc., New York, NY, 1955

(5) Bush, A. J., and Kromer, F. J., “Simplification of the Hole-Drilling Method of Residual Stress Measurements,” ISA Transaction, Vol 112, No. 3, 1973, pp. 249–260.

(6) Beaney, E. M., “Accurate Measurements of Residual Stress on Any Steel Using the Centre Hole Method,” Strain, Journal BSSM, Vol 12, No. 3, 1976, pp. 99-106.

(7) Flaman, M. T., and Herring, J. A., “Comparison of Four Hole-Producing Techniques for the Center-Hole Residual- Stress Measurement Method,” Experimental Techniques, Vol 9, No. 8, 1985, pp. 30-32.

(8) Flaman, M. T., “Investigation of Ultra-High Speed Drilling for Residual Stress Measurements by the Center Hole Method,” Experimental Mechanics, Vol 22, No. 1, 1982, pp. 26-30.

(9) Kelsey, R. A., “Measuring Non-Uniform Residual Stresses by the Hole Drilling Method,” Proceedings, SESA, Vol 14, No. 1, 1956, pp. 181-194.

(10) Sandifer, J. P., and Bowie, G. E., “Residual Stress by Blind Hole Method with Off-Center Hole,” Experimental Mechanics, Vol 18, No. 5, 1978, pp. 173-179.

(11) “Measurement of Residual Stresses by the Hole Drilling Strain Gage Method,” Tech Note TN-503-4, Measurements Group, Raleigh, NC.

(12) Schajer, G. S. “Judgment of Residual Stress Field Uniformity when Using the Hole-Drilling Method,” Proceedings of the International Conference on Residual Stresses II, Nancy, France. November 23-25, 1988, pp. 71-77.

(13) Redner, S., and Perry, C. C., “Factors Affecting the Accuracy of Residual Stress Measurements Using the Blind Hole Drilling Method,” Proceedings of 7th International Conference Experimental Stress Analysis, August 1982, pp. 604-616.

(14) Schajer, G. S. “Measurement of Non-Uniform Residual Stresses Using the Hole Drilling Method,” Journal of Engineering Materials and Technology, Vol 110, No. 4, 1988, Part I: pp. 338-343, Part II: pp. 344-349.

(15) Beaney, E. M., and Procter, E., “A Critical Evaluation of the Centre Hole Technique for the Measurement of Residual Stresses,” Strain, Vol 10, No. 1, 1974, pp. 7-14, 52.

(16) Yavelak, J. J. (compiler), “Bulk-Zero Stress Standard-AISI 1018 Carbon-Steel Specimens, Round Robin Phase 1,” Experimental Techniques, Vol 9, No. 4, 1985, pp. 38-41.

(17) Flaman, M. T., and Herring, J. A., “SEM/ASTM Round-Robin Residual-Stress- Measurement Study-Phase 1, 304 Stainless- Steel Specimen,” Experi- mental Techniques, Vol 10, No. 5, 1986, pp. 23-25.

(18) Weng, C. C., Lin, Y. C., and Chou, C. P., “A Study on the Induced Drilling Stresses in the Centre Hole Method of Residual Stress Measurement,” Strain, Vol 28, 1992, pp. 45-51.

(19) Schajer, G. S., and Tootoonian, M., “A New Rosette Design for More Reliable Hole-Drilling Residual Stress Measure- ments,” Experimental Mechanics, Vol 37, No. 3, 1997, pp. 299-306.

(20) Schajer, G. S., “Strain Data Averaging for the Hole-Drilling Method.” Experimental Techniques, Vol 15, No. 2, 1991, pp. 25-28.

(21) Lu, J. (ed.),“ Handbook of Measure- ment of Residual Stresses,” Society for Experimental Mechanics, Fairmont Press, Lilburn, GA, 1996, Chapter 2.

(22) Kroenke, W.C., Holloway, A.M., and Mabe, W.R., “Stress Calculation Update in ASTM E 837 Residual Stress Hole Drilling Standard”, Advances in Computational Engineering & Sciences, Tech Science Press, Vol. 1, 2000, p. 695-699.